Trabajo con matrices en Wiris

Para realizar cálculos con matrices en Wiris se trabaja en la pestaña de operaciones, donde hay varios comandos que, además de definir las matrices, permiten calcular su traspuesta, inversa, potencia, determinante... Para ilustrarlo, se muestran los siguientes ejemplos:

Resolucion de sistemas de ecuaciones con Wiris

• Resolución analítica

Para resolver analíticamente sistemas de ecuaciones con Wiris se trabaja en la pestaña de Operaciones con el comando "resolver sistema", con lo que aparece una ventana en la interfaz de trabajo, en la que hay que escribir el número de ecuaciones que tendrá el sistema a resolver:

Haciendo clic en “Aceptar”, aparecerá en la ventana de trabajo la expresión resolver con dos llaves entre las que se escribirán todas las ecuaciones que componen el sistema, igual que se hacía con las ecuaciones simples. Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

• Resolución gráfica

Otra forma de resolver un sistema de ecuaciones es mediante la representación gráfica de sus ecuaciones y obteniendo el punto, línea o plano de corte, con la ayuda del comando intersección. Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

Representación de funciones con Wiris

Para representar funciones con Wiris se trabaja en la pestaña de Operaciones con el comando "representar". Entre los dos paréntesis se escribirá la función que se quiere representar con la herramienta. Como ejemplo, se resuelven los siguientes ejercicios con Wiris:

En resumen, la herramienta “representar” destaca con colores aquellas características especiales que tiene cada gráfica, facilitando su análisis matemático:

- Máximos o mínimos → color rojo

- Puntos de inflexión → color verde

- Puntos de corte con los ejes X e Y → color azul

- Ejes de simetría → color verde

- Asíntotas → color azul

Cálculo de límites con Wiris

En la pestaña de Análisis se emplea el comando de límite. En el cuadrado verde mayor se escribe la expresión matemática cuyo límite se busca. En los dos cuadrados pequeños se escriben la variable y el valor hacia el que tiende dicha variable, respectivamente. Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

Estudios de divisibilidad con Wiris

• Descomposición factorial

Para hacer la descomposición factorial de un número entero se emplea la función factorizar(). Wiris devuelve la descomposición de dicho número como producto de factores primos. Dicha función también se puede emplear para factorizar polinomios con coeficientes reales. Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

• Cálculo de los divisores de un número

Para calcular los divisores de un número se emplea la función divisores(). Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

• Números primos

Para saber si un número es primo o compuesto se se emplea la función primo?(). Si el número es primo, Wiris dará como respuesta cierto; si es compuesto la respuesta será falso. Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

• Máximo común divisor y mínimo común múltiplo

Para calcular el máximo común divisor de varios números se emplea la función mcd() y para el mínimo común múltiplo la función mcm(). En ambos casos los números se separan con comas. Como ejemplo, se resuelven los siguientes ejercicios con Wiris:

 

Resolución de ecuaciones con Wiris

Comprobación de operaciones combinadas

Para realizar una operación combinada con números enteros de forma correcta, resulta esencial seguir unas pautas que respeten el orden de prioridad y racionen las operaciones a realizar en cada paso, con objeto de cuidar al máximo la precisión necesaria para llegar al resultado final correcto.

Algunas recomendaciones para trabajar estos ejercicios son:

1) Hacer las operaciones necesarias dentro de cada paréntesis, para reducir su contenido a un sólo número. Si dentro de un paréntesis hay varias sumas y/o restas, es conveniente operarlas de dos en dos. Es un método más seguro, para evitar equivocaciones.

2) Operar productos, cocientes y potencias (no hay que olvidar que estas últimas, también son productos).

3) Quitar paréntesis cuando sólo haya un número dentro de cada uno de ellos. Para ello, hay que fijarse en el signo que tienen delante (el – cambia el signo, el + no).

4) Realizar las sumas y restas finales, operando los enteros de dos en dos. Es más seguro para evitar equivocaciones.

5) Si hay algún corchete, recuerda que no tendrá sentido conservarlo como tal, cuando dentro de él no haya otros paréntesis.

6) Cada vez que se realice algún cambio, se debe escribir todo el ejercicio de nuevo, dejando lo que no se ha operado como estaba.

Aunque es cierto que hay muchas formas de realizar estos ejercicios de forma correcta, se deben dar un número mínimo de pasos que demuestren el resultado final y no es recomendable hacer demasiadas cosas a la vez, pues se corre un riesgo innecesario que puede precipitar en errores de muy diversa índole.

Como ejemplo, se resuelve el siguiente ejercicio con Wiris:

Diseño de Avatares

En el diseño de la imagen del avatar no será válida una fotografía, para preservar la privacidad del alumn@. Por lo que se sugiere diseñarla con algún programa libre del tipo DoppelMe.

Además, se deberá hacer una ficha de presentación de cada alumn@ del curso virtual en la que se incluya una ecuación matemática o expresión matemática que tenga una especial relevancia para cada uno de los alumn@s del curso virtual. A modo de ejemplo las creadoras del blog destacan la ecuación:

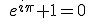
Esta ecuación es la "Identidad de Euler", que recoge los cinco números más importantes de la historia de las  matemáticas.
Su imagen se ha creado con el editor de ecuaciones al que se llega pinchando aquí.

Dicha ficha de presentación se enviará al e-mail de las profesoras, incluyendo el código HTML que permita incrustar la ecuación en una página web que proporciona el editor anterior, para su posterior publicación en el blog.
Ficha profesora Almudena


Nota: En el viewer de GoogleDocs las imágenes se ven con muy poca calidad, es necesario descargarse los documentos para verlos adecuadamente.
El objetivo final es diseñar un póster con todos los participantes en el curso con la herramienta gratuita Glogster

Mapas conceptuales

Es indiscutible la utilidad de los mapas conceptuales con el fin de potenciar el aprendizaje “significativo” frente a uno puramente memorístico y por tanto, se busca fomentar el uso de los mapas conceptuales elaborados por los propios alumnos y alumnas. Para ello se sugiere la herramienta Gliffy  y, a modo de ejemplo, se muestra el siguiente mapa conceptual:

Se sugiere a los alumn@s elaborar un mapa similar pero más completo que incluya los casos restantes, denominados por la profesora Pilar "Dra Antiferroeléctrica 4001" en el blog "Matemáticas para exploradores" casos 2 y 3 de resolución ecuaciones de segundo grado con una incógnita.
Además, se facilita a los alumnos un sencillo manual para aprender rápidamente a utilizar esa herramienta: pinchar aquí.



Algunos trabajos realizados por los alumnos son:

Comunicación on-line con las familias: "Programa bitácora"

El programa Bitácora es un recurso informático para mantener un contacto fluido por e-mail entre los profesores y los padres de sus alumnos, respetando en todo momento la ley de protección de datos. Está compartido bajo licencia GNU por sus creadores:
Pedro Luis Lucas Rosado (Profesor de Informática y asesor TIC en el IES Villablanca)
Pilar López del Castillo (Profesora de Matemáticas y Ciencias Naturales en el IES Blas de Otero)
Se puede descargar en Dropbox: Descarga el programa Bitácora

Hipótesis del universo matemático (Mathematical universe hypothesis)

De acuerdo con el físico teórico Max Tegmark "todo lo que existe matemáticamente también existe físicamente en el mundo real".
En su teoría actualiza la física cuántica y la cosmología con el concepto de muchos universos paralelos habitando en múltiples niveles del espacio y tiempo. La hipótesis del universo matemático, a medio camino entre la física y la filosofía, nos remonta a la clásica pregunta de los Griegos: ¿qué es real?
Fuentes:
Wikipedia
Noticias del cosmos

Otros recursos interesantes

Juegos matemáticos
En la web Mates y + se recogen interesantes actividades a realizar con palillos muy útiles para clase. Pincha aquí para verlos.
También podemos jugar al clásico Cifras y Letras: Pincha aquí.
Si te gusta el ahorcado prueba con uno de matemáticos célebres (pincha aquí)
o con otro de términos matemáticos en inglés (pincha aquí).


Documentales matemáticos
Con un título muy similar al del blog hemos encontrado unos interesantes vídeos.
Universo matemático consta de diez documentales de 24 minutos de duración cada uno de índole matemática, producida en el año 2000 por el programa La aventura del saber, de La 2 de Televisión Española.
Se encuentran recopilados en la web del INTEF- Instituto Nacional de Tecnologías Educativas y de Formación del Profesorado- y vienen acompañados de fichas e interesantes actividades complementarias Pincha aquí para verlos

Otra serie interesante que proponemos por su utilidad es Mas por menos.


Cálculo mental
Una actividad titulada "La máquina de calcular" para trabajar el cálculo mental en un minuto.
Pincha aquí para jugar.


Ofimática con LibreOffice
Es un software libre para la edición de documentos de texto, creación de presentaciones y dibujos, o trabajo con bases de datos. Como se explica en el blog "Las aventuras de los biofísicos", también de la profesora Pilar López del Castillo, es compatible en todo con el paquete de Microsoft Office (tradicional word, así conocido por los estudiantes), salvo en la creación y edición de fórmulas matemáticas. En dicho blog se muestra  un Vídeo-tutorial para explicar su uso básico.

La música de pi
Interesante artículo sobre el número irracional más famoso.

Video interesante
Elabora un ranking sobre las 10 ecuaciones más importantes desde el punto de vista de su contribución a la ciencia.






Troncho y poncho
Divertidos vídeos sobre potencias, fracciones y probabilidad.